INTEGRACION POR SUSTITUCION
 

El método consiste en sustituir el integrando o parte de éste por otra función para que la expresión resultante sea más fácil de integrar. Si escogemos un cambio de variable de modo que al aplicarlo obtenemos en el integrando una función multiplicada por su derivada, la integral será inmediata. Pero en ocasiones un cambio mal escogido puede complicar más la integral.

En el caso de las integrales definidas, al aplicar el cambio hay que actualizar los extremos de la integral. Por ejemplo, si los extremos de la integral inicial (con variable x) son 0 y 1 y la nueva variable es s =2x, los nuevos extremos serán 0 y 2. Notemos que de este modo el intervalo de variación de la variable es el mismo.

En esta sección resolvemos integrales indefinidas por medio de este método. Los integrandos son funciones racionales, con raíces, con funciones trigonométricas, raíces en el denominador, logaritmos...
 

Cambios de variable recomendados

En la siguiente tabla se recopilan diferentes cambios de variable que suelen funcionar en la mayoría de las integrales que nos encontraremos:
 

EJEMPLOS
 

 RESOLVER:

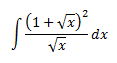
Nota 1: esta integral es en realidad inmediata, pero la vamos a resolver mediante sustitución.

Nota 2: en esta integral aplicamos dos cambios de variable para hacer notar, por un lado, que existen múltiples primitivas para una misma función. Y, por otro lado, que pueden aplicarse distintos cambios de variables. No obstante, un cambio de variable mal escogido puede complicar la integral.

SOLUCION:
 

La idea es aplicar un cambio de variable de modo que los signos radicales desaparezcan. Esto se consigue, por ejemplo, con el cambio

Cambio de variable 1:

$$z=\sqrt{x}$$

Aislamos x en la expresión anterior elevando al cuadrado:

$$x=z^2$$

Derivamos:

$$dx=2zdz$$

Aplicamos el cambio en la integral:

$$\int \frac{(1+\sqrt{x}{)}^2}{\sqrt{x}}dx=\int \frac{(1+z{)}^2}{z}\cdot 2zdz=$$

$$=\int (1+z{)}^2\cdot 2dz=2\int (1+z{)}^{2}dz$$

Desarrollamos el cuadrado de la suma para escribir la integral de la suma como la suma de las integrales:

$$2\int (1+z{)}^{2}dz=2\left(\int 1dz+\int z^{2}dz+\int 2zdz\right)=$$

$$=2\left(z+\frac{z^3}{3}+z^2\right)=2z+\frac{2z^3}{3}+2z^2$$

Finalmente, deshacemos el cambio de variable, lo que significa escribir es el resultado en función de la variable inicial, es decir, x.

$$z=\sqrt{x}\to z^2=x,z^3=(\sqrt{x}{)}^3$$

Por tanto,

$$\int \frac{(1+\sqrt{x}{)}^2}{\sqrt{x}}dx=2\sqrt{x}+\frac{2(\sqrt{x}{)}^3}{3}+2x+C$$

donde C es la constante de integración.

Cambio de variable 2:

$$z=1+\sqrt{x}$$

Con este cambio también desaparecen las raíces.

Aislamos x y derivamos:

$$x=(z-1{)}^2$$

$$dx=2(z-1)dz$$

Aplicamos el cambio en la integral:

$$\int \frac{(1+\sqrt{x}{)}^2}{\sqrt{x}}dx=\int \frac{(z{)}^2}{z-1}\cdot 2(z-1)dz=$$

$$=\int 2z^{2}dz=\frac{2z^3}{3}$$

Deshacemos el cambio de variable:

$$\int \frac{(1+\sqrt{x}{)}^2}{\sqrt{x}}dx=\frac{2(1+\sqrt{x}{)}^3}{3}+C$$

Nota: las dos funciones primitivas obtenidas son distintas, pero sus respectivas derivadas son iguales.